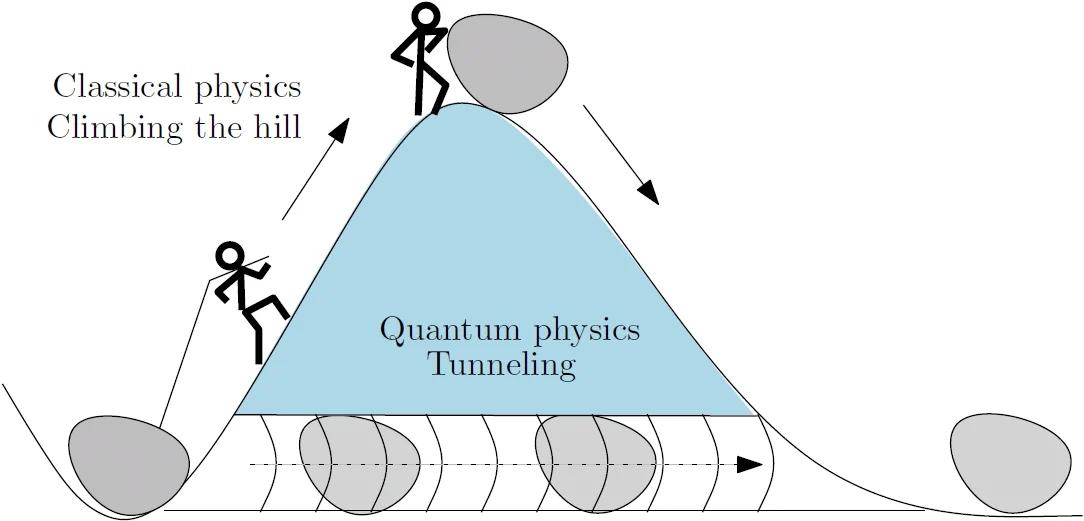
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
| from manim import *
import numpy as np
def generate_spatial_grid(num_points: int, domain_half_length: float) -> tuple[np.ndarray, float]:
"""
生成空间网格与网格间距。
- num_points: 空间采样点数(建议为 2 的幂)
- domain_half_length: 空间范围的一半 L,使得 x ∈ [-L, L]
返回:
x: 形如 [-L, ..., L) 的等距网格
dx: 网格间距
"""
x = np.linspace(-domain_half_length, domain_half_length, num_points, endpoint=False)
dx = x[1] - x[0]
return x, dx
def generate_wavenumbers(num_points: int, dx: float) -> np.ndarray:
"""
生成与 FFT 对应的波数数组 k(与 numpy.fft.fftfreq 一致的排列)。
"""
freqs = np.fft.fftfreq(num_points, d=dx)
k = 2.0 * np.pi * freqs
return k
def build_potential_barrier(x: np.ndarray, barrier_left: float, barrier_right: float, barrier_height: float) -> np.ndarray:
"""
有限方势垒:
V(x) = barrier_height, x ∈ [barrier_left, barrier_right]
0, 其他
"""
V = np.zeros_like(x)
mask = (x >= barrier_left) & (x <= barrier_right)
V[mask] = barrier_height
return V
def build_initial_plane_wave(x: np.ndarray, k0: float, amplitude: float = 1.0) -> np.ndarray:
"""
平面波 ψ(x,0) = A * exp(i k0 x),不进行空间归一化。
模拟从无限远传播的平面波。
"""
psi = amplitude * np.exp(1j * k0 * x)
return psi
def build_initial_wave_packet_from_left(x: np.ndarray, k0: float, amplitude: float = 1.0,
packet_center: float = -30.0, packet_width: float = 3.0) -> np.ndarray:
"""
创建一个从左侧传播进来的波包,模拟平面波从无限远传播的效果。
使用高斯包络来限制初始波包的位置,让它从左侧逐渐传播进来。
"""
gaussian_envelope = np.exp(-((x - packet_center) ** 2) / (2.0 * (packet_width ** 2)))
plane_wave_phase = np.exp(1j * k0 * x)
psi = amplitude * gaussian_envelope * plane_wave_phase
return psi
def build_initial_gaussian_packet(x: np.ndarray, center: float, width: float, k0: float) -> np.ndarray:
"""
高斯波包 ψ(x,0) ~ exp(-(x-x0)^2/(4σ^2)) * exp(i k0 x),并进行 L2 归一化。
"""
gaussian_envelope = np.exp(-((x - center) ** 2) / (4.0 * (width ** 2)))
plane_wave_phase = np.exp(1j * k0 * x)
psi = gaussian_envelope * plane_wave_phase
norm = np.sqrt(np.trapz(np.abs(psi) ** 2, x))
psi /= norm
return psi
def split_step_fourier_time_evolution(
psi0: np.ndarray,
potential: np.ndarray,
time_step_sim: float,
num_sim_steps: int,
dx: float,
k_array: np.ndarray,
store_stride: int,
) -> tuple[np.ndarray, np.ndarray]:
"""
分步傅里叶法时间推进:
ψ(t+dt) ≈ e^{-iV dt/2} F^{-1}[ e^{-i k^2 dt / (2m)} F[e^{-iV dt/2} ψ(t)] ]
此处取 ℏ=1, m=1。
- psi0: 初始 ψ(x)
- potential: V(x)
- time_step_sim: 数值仿真时间步长 dt(较小以稳定)
- num_sim_steps: 总仿真步数 Nsteps
- dx: 空间网格间距
- k_array: 与 FFT 匹配的波数数组
- store_stride: 每隔多少个仿真步保存一次数据
返回:
times_saved: shape (Nsaved,)
psi_saved: shape (Nsaved, N), 复数 数组(可据此计算 |ψ|²)
"""
num_points = psi0.size
exp_halfV = np.exp(-1j * potential * (time_step_sim / 2.0))
expT = np.exp(-1j * (k_array ** 2) * (time_step_sim / 2.0))
psi = psi0.astype(np.complex128, copy=True)
num_saved = (num_sim_steps // store_stride) + 1
psi_saved = np.zeros((num_saved, num_points), dtype=np.complex128)
times_saved = np.zeros(num_saved, dtype=np.float64)
save_index = 0
psi_saved[save_index, :] = psi
times_saved[save_index] = 0.0
save_index += 1
for step in range(1, num_sim_steps + 1):
psi *= exp_halfV
psi_k = np.fft.fft(psi)
psi_k *= expT
psi = np.fft.ifft(psi_k)
psi_k = np.fft.fft(psi)
psi_k *= expT
psi = np.fft.ifft(psi_k)
psi *= exp_halfV
if (step % store_stride) == 0:
psi_saved[save_index, :] = psi
times_saved[save_index] = step * time_step_sim
save_index += 1
psi_saved = psi_saved[:save_index, :]
times_saved = times_saved[:save_index]
return times_saved, psi_saved
class QuantumBarrierInfinity(Scene):
def construct(self) -> None:
num_points = 4096
L = 100.0
x, dx = generate_spatial_grid(num_points, L)
k = generate_wavenumbers(num_points, dx)
barrier_left = -7.0
barrier_right = 7.0
barrier_height = 2.0
V = build_potential_barrier(x, barrier_left, barrier_right, barrier_height)
k0 = 1.5
amplitude = 0.5
packet_center = -30.0
packet_width = 3.0
psi0 = build_initial_wave_packet_from_left(x, k0, amplitude, packet_center, packet_width)
t_max = 20.0
dt_sim = 1e-3
total_steps = int(t_max / dt_sim)
target_fps = 60.0
dt_store = 1.0 / target_fps
store_stride = max(1, int(round(dt_store / dt_sim)))
times, psi_saved = split_step_fourier_time_evolution(
psi0=psi0,
potential=V,
time_step_sim=dt_sim,
num_sim_steps=total_steps,
dx=dx,
k_array=k,
store_stride=store_stride,
)
density_saved = (np.abs(psi_saved) ** 2).astype(np.float64)
density_max = float(np.max(density_saved))
y_max = max(0.3, min(0.8, density_max * 1.3))
display_range = 25.0
axes = Axes(
x_range=[-display_range, display_range, 3.0],
y_range=[0.0, y_max, y_max / 8.0],
x_length=12.0,
y_length=5.3,
axis_config={
"include_numbers": True,
"font_size": 24,
"decimal_number_config": {"num_decimal_places": 2}
},
tips=False,
).to_edge(DOWN, buff=0.8)
for number in axes.y_axis.numbers:
number.shift(LEFT * 0.3)
title = Tex("Quantum Tunneling through Finite Potential Barrier").to_edge(UP, buff=0.5)
barrier_display_height = barrier_height * 0.3
barrier_polygon = Polygon(
axes.c2p(barrier_left, 0.0, 0.0),
axes.c2p(barrier_right, 0.0, 0.0),
axes.c2p(barrier_right, barrier_display_height, 0.0),
axes.c2p(barrier_left, barrier_display_height, 0.0),
color=YELLOW,
fill_opacity=0.3,
stroke_opacity=0.8,
)
barrier_label = Tex("Barrier", font_size=24).next_to(barrier_polygon, UP, buff=0.1)
time_tracker = ValueTracker(0.0)
x_values = x
def build_density_graph() -> Mobject:
current_t = time_tracker.get_value()
max_index = len(times) - 1
dt_store_effective = times[1] - times[0] if len(times) > 1 else 1.0 / 60.0
index = int(np.clip(round(current_t / dt_store_effective), 0, max_index))
y_values = density_saved[index]
mask = (x >= -display_range) & (x <= display_range)
x_display = x[mask]
y_display = y_values[mask]
graph = axes.plot_line_graph(
x_values=x_display,
y_values=y_display,
add_vertex_dots=False,
line_color=BLUE,
stroke_width=3,
)
return graph
density_graph = always_redraw(build_density_graph)
time_label = always_redraw(
lambda: Tex(f"t = {time_tracker.get_value():.2f} s", font_size=32).next_to(axes, DOWN, buff=0.3)
)
params_text = VGroup(
Tex(f"Initial Energy: {k0**2/2:.2f}", font_size=20),
Tex(f"Potential Barrier Height: {barrier_display_height:.2f}", font_size=20),
).arrange(DOWN, aligned_edge=LEFT).to_edge(LEFT, buff=2.5)
self.add(title, axes, barrier_polygon, barrier_label, density_graph, time_label, params_text)
initial_text = Tex("Wave Propagate from left", font_size=28).to_edge(RIGHT, buff=1.5)
self.add(initial_text)
self.play(
time_tracker.animate.set_value(float(times[-1])),
run_time=float(times[-1]),
rate_func=linear
)
self.remove(initial_text)
self.wait(2)
|