复现与展望——源自几何对凸粒子普适的公式

引入

我们讨论的硬凸粒子系统，其相互作用势是一种排斥性的$\delta$势，具有一定的“纯粹性”。原论文将注意力放在一个源自几何关系的对所有凸粒子皆成立的恒等式上，采用python的软件包HOOMD-bule完成对问题的模拟，我也跟随相同的路线进行工作。在复现完成后，我将视线放到凹粒子的群上，它们的研究方法相似，不过凹粒子的属性更加多样，许多常见的物品实际上是凹的，如字母H，五角星等等。

我们回到关键的恒等式上来

$$\lim_{\substack{N \to \infty \\ N/V =\rho}} \, \frac{1}{N} \ln (\prod_{i=1}^{N} \frac{P_{N+1}}{P_{i}} ) = -\frac{\tilde{s}(0+) }{2d}.$$

指定分子数密度N，调整密度为$N/V=\rho$ ，此时固定V，可以开始研究从1到N的粒子数在这样的V下随机组合的粒子群，我们在某些数目的粒子群中执行插入一个粒子的操作从而得到插入粒子的概率$P_i$，即为在$i-1$个粒子的群中插入一个粒子的成功率。

等式右侧的$\tilde{s}(x)$为尺寸分布函数，在原论文中有详细介绍。$\mathrm{d}$则是空间的维度。

环境配置

在conda环境下进行HOOMD-blue包的安装，具体参见HOOMD-blue的安装教程。需要注意的是HOOMd-blue需要Linux环境，并且在利用WSL实现的虚拟机无法调用GPU进行运算，代码开源于github,可以通过终端命令下载源码

git clone https://github.com/glotzerlab/hoomd-blue.git

代码构建

主体架构

完成论文的代码开源于https://github.com/old-cabbage/Particle-Move-with-HOOMD-blue，架构如下

Particle/
├─concave    
├─convex  
├─mixture  
└─result
    ├─concave
    ├─convex
    └─sdf
        ├─concave     
        ├─convex      
        └─mixture

system.py文件将粒子群本身作为一个类，将论文所需要的操作变为类本身的函数，可以大大简化调整关键参数的修改过程。主要需要修改的文件是 particle-move. py，通过调整相应的粒子种类，实验需要模拟的次数来实现。这里我们的粒子群实际是以.gsd文件保存的，由于需要生成大量的.gsd文件，故采用generate.py文件独立地生成粒子群，可以减少主程序的负担。result文件夹存放着蒙特卡洛模拟的结果，concave、convex文件夹中都有进行数据分析所需要的文件，可以快捷进行数据的可视化。

关键方法

并行

实现项目的计算量较大，一般需要在高算力服务器上进行，且很多工作是可以并行而不影响结果的，故文件都进行了适当的MPI并行处理，

在System类中，采用了两种方法生成粒子群，一种是直接让粒子在既定密度下有序排列，再执行打乱操作，增大粒子群的熵，适合密度不大和凸粒子的情况；另一种则是利用hoomd.hpmc.update中的QuickCompress类，添加其到Simulation.operations.updaters方法中，通过指定压缩方式和速度，可以实现逐步的将密度较小的体系压缩成高密度体系，并且体系的熵自然的增高。

#压缩体系
initial_box = self.simulation.state.box
final_box = hoomd.Box.from_box(initial_box)
final_box.volume = self.simulation.state.N_particles * self.particle_area / self.packing_density
compress = hoomd.hpmc.update.QuickCompress(
    trigger=hoomd.trigger.Periodic(10), target_box=final_box
)
self.simulation.operations.updaters.append(compress)
periodic = hoomd.trigger.Periodic(10)
tune = hoomd.hpmc.tune.MoveSize.scale_solver(
    moves=["a", "d"],
    target=0.2,
    trigger=periodic,
    max_translation_move=5,
    max_rotation_move=5,
)
self.simulation.operations.tuners.append(tune)

插入操作

HOOMD-blue的hpmc中提供了FreeVolume方法计算体系的剩余体积，它是通过不断投入粒子实现的，故通过简单改变投入粒子的类型再对结果做一些处理即可得到需要的成功率

def random_insert(self,insert_times):
self.fv=hoomd.hpmc.compute.FreeVolume(test_particle_type=self.shape, 
num_samples=insert_times)
self.simulation.operations.computes.append(self.fv)
self.success_insert = round(self.fv.free_volume * 
insert_times / self.simulation.state.box.volume)
return self.success_insert

在主程序中通过循环实现插入并更新体系的蒙特卡洛操作

iterations = 1000              # 循环次数
moves_per_cycle = 5            # 每个循环中移动的步数
insertions_per_cycle = 100000    # 每个循环中插入的粒子尝试次数

total_success = 0
total_attempts = 0

print("\n开始进行循环模拟和插入测试...")
simulation_start_time = time.time()
for cycle in range(1, iterations + 1):
    # 进行移动
    system.simulation.run(moves_per_cycle)
    
    # 进行插入尝试  
    success = system.random_insert(
        insert_times=insertions_per_cycle
    )
    total_success += success
    total_attempts += insertions_per_cycle

    # 可选：打印每个循环的结果
    if cycle % (iterations // 10 ) == 0:
        simulation_interval_time = time.time()
        print(f"循环 {cycle}/{iterations}: 成功插入 {success}/{insertions_per_cycle} 个粒子;
        耗时: {simulation_interval_time - simulation_start_time:.2f} 秒")

simulation_end_time = time.time()
print(f"\n堆叠密度为{packing_density_0}，粒子数为{num_particles}的循环模拟和插入测试完成，
耗时: {simulation_end_time - simulation_start_time:.2f} 秒")
# 计算最终的成功插入概率
final_probability = total_success / total_attempts if total_attempts > 0 else 0.0
print(f"最终插入成功概率: {final_probability * 100:.5f}% ({total_success}/{total_attempts}) ;
ln(Pi)={math.log(final_probability)}")

SDF计算

SDF的计算调用了HOOMD-blue的SDF函数，可以获得曲线，也可以直接SDF.P来直接计算SDF的截距，在system文件中通过以下操作实现

def calculate_sdf(self,sdf_mc,sdf_xmax,sdf_dx,sdf_each_run):
    self.total_sdf_sdfcompression=np.zeros(int(sdf_xmax/sdf_dx))
    self.total_sdf_sdfexpansion=np.zeros(int(sdf_xmax/sdf_dx))
    self.sdf_compute = hoomd.hpmc.compute.SDF(xmax=sdf_xmax, dx=sdf_dx)
    self.simulation.operations.computes.append(self.sdf_compute)
    #sdf_start_time=time.time()
    print("sdf循环开始")
    for i in range(sdf_mc):
        self.simulation.run(sdf_each_run)
        self.total_sdf_sdfcompression += self.sdf_compute.sdf_compression
        self.total_sdf_sdfexpansion += self.sdf_compute.sdf_expansion
        #if (i+1)%(sdf_mc//10)==0:
        #    sdf_interval_time=time.time()
        #    print(f"循环已经进行了{i+1}次,耗时{sdf_interval_time-sdf_start_time:.2f}秒")
    self.total_sdf_xcompression = self.sdf_compute.x_compression
    self.total_sdf_xexpansion = self.sdf_compute.x_expansion
    self.total_sdf_sdfcompression /= sdf_mc
    self.total_sdf_sdfexpansion /= sdf_mc
    return self.total_sdf_xcompression,self.total_sdf_xexpansion,self.total_sdf_sdfcompression,self.total_sdf_sdfexpansion

凸粒子的实验结果

插入概率

与原论文相同，采用N=5000个粒子，每个数据点经过$10^9$以上次插入，得到$\mathrm{ln}(P_i)$随着粒子数增加的图线，当体系的密度过大时，$P_i$ 以极快的速度减小，在高密度体系中插入粒子十分困难，概率难以计算。

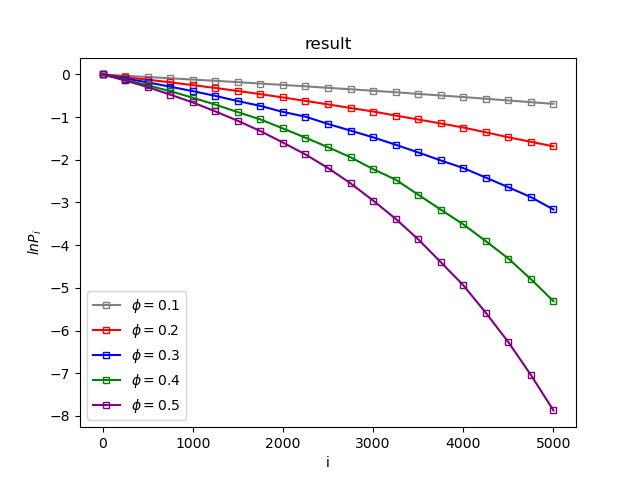
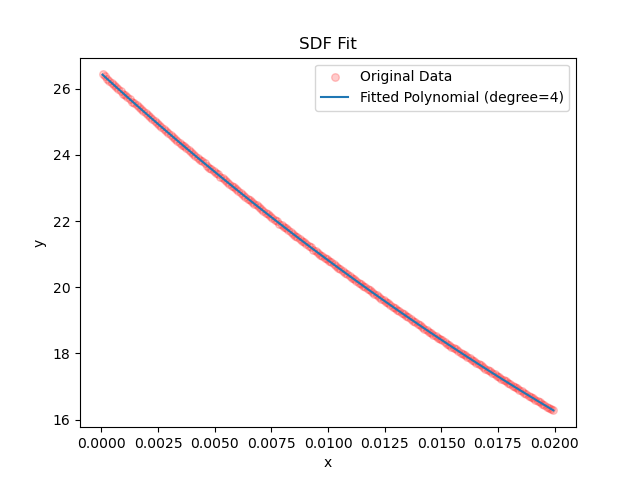
特别的，用四次曲线拟合$\mathrm{ln}(P_i)$可以获取曲线的部分性质，这里密度为0.5的曲线的四次拟合与论文中的数据相符合。

$$\mathrm{ln}(P_i)=-1.712\times10^{-15} i^4 - 1.697\times 10^{-11} i^3 - 7.424\times 10^{-8} i^2 - 5.721\times 10^{-3} i$$

SDF

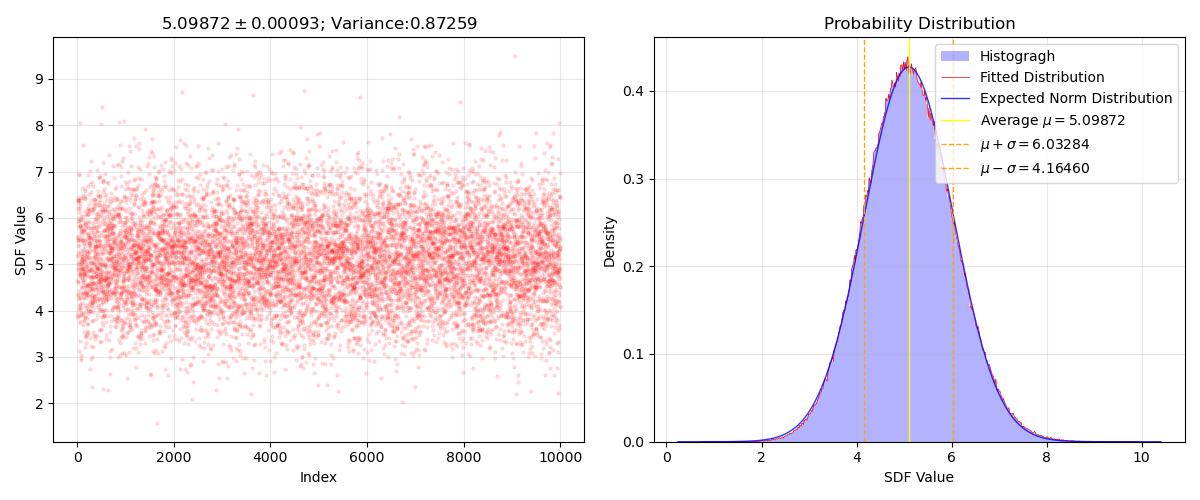
SDF计算结果的关键的横坐标与原论文相符合，这里亦选取密度为0.5的体系来分析，左图为随机选取了$10^4$个体系的SDF结果可视化的散点图，右图为根据原数据（$10^{9}$次SDF数值）而拟合出的正态曲线，与预期的标准正态曲线十分接近。

凹粒子的展望

凹粒子由于粒子形状复杂，并且库的优化弱于凸粒子，故计算难度远大于凸粒子，由于凹粒子的形态复杂，要研究凹粒子的问题势必要分析多种凹粒子的性质。一个与凸粒子不同地方是凹粒子的SDF不只有膨胀的SDF，还有压缩的SDF，在我们研究的恒等式上要加上一项。

$$\lim_{\substack{N \to \infty \\ N/V =\rho}} \, \frac{1}{N} \ln (\prod_{i=1}^{N} \frac{P_{N+1}}{P_{i}} ) = -\frac{\tilde{s}(0+) + \tilde{s}(0-)}{2d}.$$

可是，这一项并不一定在所有凹粒子上都显现，对于H粒子，由于它非常的“凹”，可以观测到$\tilde{s}(0-)$项；但是对于V字粒子，它不是很“凹”，额外的这一项完全无法对压缩造成影响

对V字粒子的结果，我们进行了较为精确的计算，结果与公式符合的很好；对于H粒子，我们进行了定性的计算，发现密度较大时插入概率十分小，SDF的膨胀项对结果产生了显著的影响。由于计算能力受限，对个别密度的验证符合公式

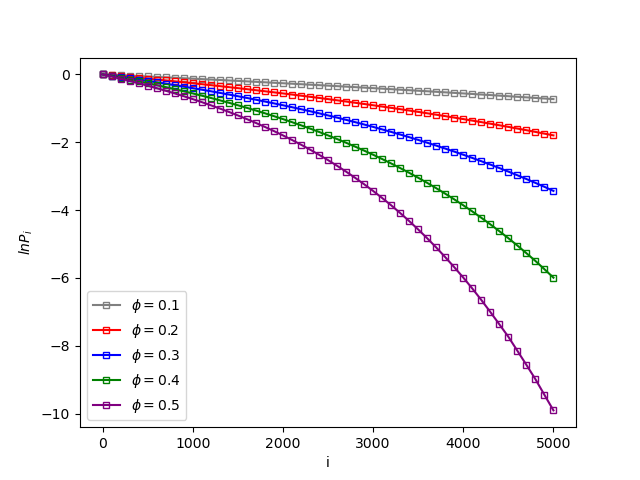
这项研究揭示了硬粒子系统中几何学和热力学之间复杂的相互作用。从熵、压强和化学势之间联系的基本热力学关系中出发，走到一个意料之外的地方，建立了一种对各种粒子成立的等式。