计算物理之简谐振动

讨论误差的影响

考虑一个单摆我们可以先解析的求解

$F_\theta=-m g \sin \theta,$ $F_\theta=m d^2s/dt^2$ $\sin \theta \approx \theta$ $\frac{d^2 \theta}{d t^2}=-\frac{g}{\ell} \theta$

解析解

$\theta=\theta_0 \sin (\Omega t+\phi)$

这里 $\omega$ 是角速度

$\Omega=\sqrt{g / \ell}$ $\begin{aligned} & \frac{d \omega}{d t}=-\frac{g}{\ell} \theta, \\ & \frac{d \theta}{d t}=\omega, \end{aligned}$

二阶常微分方程数值求解方式是类似的。

$\begin{aligned} \omega_{i+1} & =\omega_i-\frac{g}{\ell} \theta_i \Delta t, \\ \theta_{i+1} & =\theta_i+\omega_i \Delta t . \end{aligned}$

写出对应的程序

json文档

{
    "pendulum1":{
        "length":2.0,
        "theta0":3.0,
        "omega0": 0.0
    }
}

# Simulation of pendulum
import pickle
import matplotlib.pyplot as plt
import numpy as np
import json

# declare contants
g = 9.8
dt = 0.1
max_steps = 1000

# declare pendulum class
class Simple_Pendulum:
    def __init__(self, length, theta0=0, omega0=0):
        self.length = length
        self.theta = np.zeros(max_steps + 1, dtype = np.float64)
        self.omega = np.zeros(max_steps + 1, dtype = np.float64)
        self.t = np.zeros(max_steps + 1, dtype = np.float64)
        self.theta[0] = theta0
        self.omega[0] = omega0
    def calculate(self):
        for i in range(max_steps):
            self.theta[i + 1], self.omega[i + 1], self.t[i + 1] = self.move_one_step(self.theta[i], self.omega[i], self.t[i])
    def move_one_step(self, theta, omega, t):
        _theta = theta + omega*dt
        _omega = omega - (g/self.length)*theta*dt
        _t = t + dt
        return _theta, _omega, _t
    def get_results(self):
        return self.theta, self.omega, self.t

def show_pendulum():
    with open("./computational-physics-project/lecture-3/pendulum.json", "r") as f:
        data = json.load(f)
    pendulum1 = Simple_Pendulum(data["pendulum1"]["length"],
                                data["pendulum1"]["theta0"],
                                data["pendulum1"]["omega0"])
    pendulum1.calculate()
    fig, ax = plt.subplots(2, 1, layout="constrained")
    theta, omega, t = pendulum1.get_results()
    ax[0].plot(t, theta, label=r"$\theta$")
    ax[0].set(xlabel="t(s)", ylabel=r"$\theta$(m)")
    ax[0].legend()
    ax[0].set_title(r"Oscillation of $\theta$")
    ax[1].plot(t, omega, label=r"$\omega$")
    ax[1].set(xlabel="t(s)", ylabel=r"$\omega$(m/s)")
    ax[1].legend()
    ax[1].set_title(r"Oscillation of $\omega$")
    plt.savefig("pendulum.png")
    plt.show()

show_pendulum()

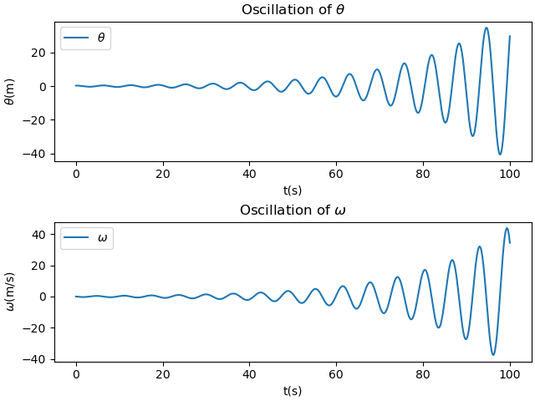
pendulum

很明显，这样处理会导致结果发散

结果发散的原因

是体系的能量不守恒

$E=\frac{1}{2} m \ell^2 \omega^2+m g \ell(1-\cos \theta) .$

小 $\theta$ 有近似

$E=\frac{1}{2} m \ell^2\left(\omega^2+\frac{g}{\ell} \theta^2\right) .$

使用欧拉方法进行转化

$E_{i+1}=E_i+\frac{1}{2} m g \ell\left(\omega_i^2+\frac{g}{\ell} \theta_i^2\right)(\Delta t)^2$

其实只需要使用 $x{i+1}=x_i+v{i+1}dt$ 代替 $x{i+1}=x_i+v{i}dt$ 就可以一定程度上解决

使用Euler-Cromer方法进行模拟

对于简谐运动，运动方程的一般形式为

$\frac{d^2x}{dt^2}=-kx^\alpha$

采用 Euler-Cromer 方法求解 x 关于时间的函数，其中 $\alpha=1$ （为了方便，取 k=1 ）。这是简谐运动的一个关键特征。然后将程序扩展到处理 $\alpha=3$ 的情况。这是一个非简谐振子的例子。计算了几个不同振幅（在范围 0.2 到 1 内）下的振动周期，并证明现在运动的周期取决于振幅。

$\alpha=1$ 的情况

谐振子的 json 文档为

{
    "oscillator":
        {
            "oscillator1":{
                "distance0":1.0,
                "velocity0":0
            },
            "oscillator2":{
                "distance0":0.2,
                "velocity0":0
            },
            "oscillator3":{
                "distance0":0.4,
                "velocity0":0
            },
            "oscillator4":{
                "distance0":0.6,
                "velocity0":0
            },
            "oscillator5":{
                "distance0":0.8,
                "velocity0":0
            }
        }
}

我们要研究这个函数的图像

$\frac{d^2x}{dt^2}=-kx^\alpha$

先只取 $\alpha=1$ ,并且 $k=1$

# Simulation of pendulum with Euler Cromer
import pickle
import matplotlib.pyplot as plt
import numpy as np
import json


# declare contants
k=1
dt = 0.1
max_steps = 1000

class simple_oscillator:
    def __init__(self, distance0=0, velocity0=0):
        self.distance = np.zeros(max_steps + 1, dtype = np.float64)
        self.velocity = np.zeros(max_steps + 1, dtype = np.float64)
        self.t = np.zeros(max_steps + 1, dtype = np.float64)
        self.distance[0] = distance0
        self.velocity[0] = velocity0
    def calculate(self):
        for i in range(max_steps):
            self.distance[i + 1], self.velocity[i + 1], self.t[i + 1] = self.move_one_step(self.distance[i], self.velocity[i], self.t[i])
    def move_one_step(self, distance, velocity, t):
        _velocity = velocity - k*distance*dt
        _distance = distance + _velocity*dt
        _t = t + dt
        return _distance, _velocity, _t
    def get_results(self):
        return self.distance, self.velocity, self.t

def show_oscillator_with_Euler_Cromer():
    with open("oscillator.json", "r") as f:
        data = json.load(f)
    oscillator1 = simple_oscillator(data["oscillator1"]["distance0"],
                                data["oscillator1"]["velocity0"])
    oscillator1.calculate()
    fig, ax = plt.subplots(2, 1, layout="constrained")
    distance, velocity, t = oscillator1.get_results()
    ax[0].plot(t, distance, label=r"$x$")
    ax[0].set(xlabel="t(s)", ylabel=r"$x$(m)")
    ax[0].legend()
    ax[0].set_title(r"Oscillation of $x$")
    ax[1].plot(t, velocity, label=r"$v$")
    ax[1].set(xlabel="t(s)", ylabel=r"$v$(m/s)")
    ax[1].legend()
    ax[1].set_title(r"Oscillation of $v$")
    plt.savefig("osillator.png")
    plt.show()

show_oscillator_with_Euler_Cromer()

当$\alpha=1$时得到图像1

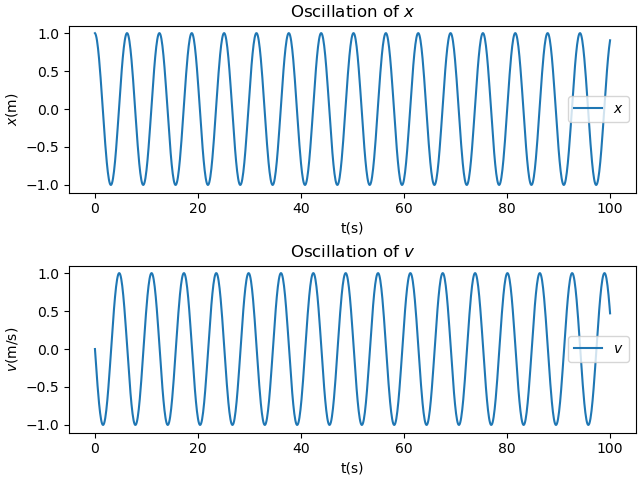
"谐振子图像1"

当$\alpha=3$时得到图像2

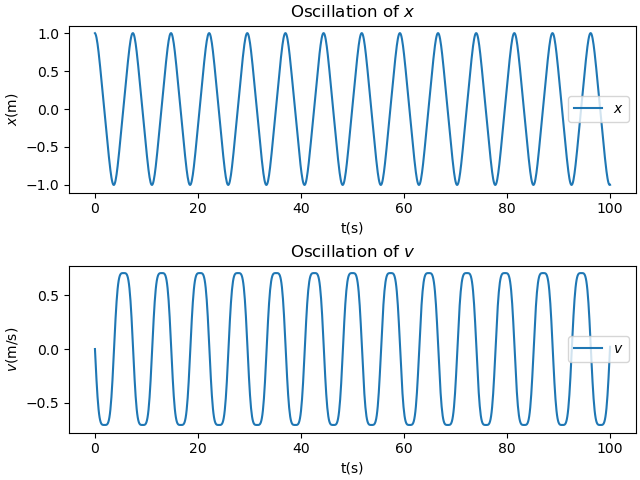
"谐振子图像2"

考虑振幅与周期的关系

接下来我们给simple_oscillator类增加一个calculate_period()函数，用来计算谐振子的周期

calculate_period() 是通过判断$x$是否在初始位置附近来确定周期大小

# Simulation of oscillators with Euler Cromer
import pickle
import matplotlib.pyplot as plt
import numpy as np
import json


# declare contants
k=1
dt = 0.1
max_steps = 1000

class simple_oscillator:
    def __init__(self, distance0=0, velocity0=0):
        self.distance = np.zeros(max_steps + 1, dtype = np.float64)
        self.velocity = np.zeros(max_steps + 1, dtype = np.float64)
        self.t = np.zeros(max_steps + 1, dtype = np.float64)
        self.distance[0] = distance0
        self.velocity[0] = velocity0
    def calculate(self):
        for i in range(max_steps):
            self.distance[i + 1], self.velocity[i + 1], self.t[i + 1] = self.move_one_step(self.distance[i], self.velocity[i], self.t[i])
    def move_one_step(self, distance, velocity, t):
        _velocity = velocity - k*distance**3*dt
        _distance = distance + _velocity*dt
        _t = t + dt
        return _distance, _velocity, _t
    def get_results(self):
        return self.distance, self.velocity, self.t,self.period
    def calculate_period(self):
        period_list=[]
        period_sum=0
        for i in range(max_steps):
            self.distance[i + 1], self.velocity[i + 1], self.t[i + 1] = self.move_one_step(self.distance[i], self.velocity[i], self.t[i])
            if i>=5 and abs(self.distance[i]-self.distance[0]) <= 0.05 and abs(self.distance[i-1]-self.distance[0]) >= 0.05:
                period_list.append(i)
        for i in range(len(period_list)):
            if i==0:
                period_sum+=period_list[0]
            else:
                period_sum+=period_list[i]-period_list[i-1]
        self.period=period_sum*dt/len(period_list)

def show_oscillator_with_Euler_Cromer():
    with open("./computational-physics-project/lecture-3/oscillator.json", "r") as f:
        data = json.load(f)
    oscillator1 = simple_oscillator(data["oscillator"]["oscillator1"]["distance0"],
                                data["oscillator"]["oscillator1"]["velocity0"])
    oscillator1.calculate_period()
    fig, ax = plt.subplots(2, 1, layout="constrained")
    distance, velocity, t , period= oscillator1.get_results()
    ax[0].plot(t, distance, label=r"$x$")
    ax[0].set(xlabel="t(s)", ylabel=r"$x$(m)")
    ax[0].legend()
    ax[0].set_title(r"Oscillation of $x$")
    ax[1].plot(t, velocity, label=r"$v$")
    ax[1].set(xlabel="t(s)", ylabel=r"$v$(m/s)")
    ax[1].legend()
    ax[1].set_title(r"Oscillation of $v$")
    plt.savefig("osillator.png")
    print(period)
    plt.show()

show_oscillator_with_Euler_Cromer()

模拟得到

振幅	周期
0.2	35.20
0.4	18.28
0.6	12.26
0.8	9.22
1.0	7.38

随着振幅增大，周期变小。

一个直观的理解，当$\alpha>1 $ 时，$-kx^\alpha$ 对 $x$ 更敏感，当$x$增大，波动会更强烈

理论解释

对于前一个练习中 (3.9) 的非简谐振子，可以通过某些特殊函数来解析地获得振动周期关于 $\alpha$ 的一般值的关系。请进行这样的计算，并描述周期与振幅之间的关系如何取决于 $\alpha$ 的值。你能对这个结果给出一个物理解释吗？提示：如果将 (3.9) 的两边都乘以 $\frac{d x}{d t}$，然后对 $t$ 进行积分。这将导致速度和 x 之间的关系。

$\frac{dv}{dt}=-kx^\alpha$

变换为

$\frac{dv}{dx}\frac{dx}{dt}=-kx^\alpha$ $vdv=-kx^\alpha dx$

积分得

$\frac{1}{2}v^2=-\frac{k}{\alpha+1}x^{\alpha+1}\bigg |_{t=0}^{t=t}$

再利用$v=\frac{dx}{dt}$

$\frac{dx}{dt}=\sqrt{\frac{2k}{\alpha+1}(x^{\alpha+1}-x_0^{\alpha+1})}$ $\frac{dx}{\sqrt{x^{\alpha+1}-x_0^{\alpha+1})}}=\sqrt{\frac{2k}{\alpha+1}}dt$

这个积分无法解析表示，但是可以写成下式

$x=F(\sqrt{\frac{2k}{\alpha+1}}t)$

其中$F(x)$是一个周期函数

那么$\sqrt{\frac{2k}{\alpha+1}}$随$\alpha$增大而减小，故周期增大